LEY DE OHM
La Ley de Ohm afirma que la corriente que circula por un conductor eléctrico es directamente proporcional a la tensión e inversamente proporcional a la resistencia siempre y cuando su temperatura se mantenga constante.
La ecuación matemática que describe esta relación es:
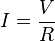 Donde, I es la corriente que pasa a través del objeto en amperios, V es la diferencia de potencial de las terminales del objeto en voltios, y R es la resistencia en ohmios (Ω). Específicamente, la ley de Ohm dice que la R en esta relación es constante, independientemente de la corriente.
Esta ley tiene el nombre del físico alemán Georg Ohm, que en un tratado publicado en 1827, halló valores de tensión y corriente que pasaba a través de unos circuitos eléctricos simples que contenían una gran cantidad de cables. Él presentó una ecuación un poco más compleja que la mencionada anteriormente para explicar sus resultados experimentales. La ecuación de arriba es la forma moderna de la ley de Ohm.
La relación entre voltaje, corriente y resistencia se compara por analogía con un circuito eléctrico y uno hidráulico. Cuando se aumenta la fuerza electromotriz, se aumenta la corriente, entonces se dice que la corriente es directamente proporcional al voltaje, si aumentamos al doble el voltaje la corriente crecerá también el doble. También la corriente es inversamente proporcional a la resistencia, en este caso, si la resistencia se hace mayor, la corriente se hará menor.
RESISTENCIA
Donde, I es la corriente que pasa a través del objeto en amperios, V es la diferencia de potencial de las terminales del objeto en voltios, y R es la resistencia en ohmios (Ω). Específicamente, la ley de Ohm dice que la R en esta relación es constante, independientemente de la corriente.
Esta ley tiene el nombre del físico alemán Georg Ohm, que en un tratado publicado en 1827, halló valores de tensión y corriente que pasaba a través de unos circuitos eléctricos simples que contenían una gran cantidad de cables. Él presentó una ecuación un poco más compleja que la mencionada anteriormente para explicar sus resultados experimentales. La ecuación de arriba es la forma moderna de la ley de Ohm.
La relación entre voltaje, corriente y resistencia se compara por analogía con un circuito eléctrico y uno hidráulico. Cuando se aumenta la fuerza electromotriz, se aumenta la corriente, entonces se dice que la corriente es directamente proporcional al voltaje, si aumentamos al doble el voltaje la corriente crecerá también el doble. También la corriente es inversamente proporcional a la resistencia, en este caso, si la resistencia se hace mayor, la corriente se hará menor.
RESISTENCIA
La resistencia eléctrica de un conductor depende de tres factores que quedan recogidos en la ecuación que sigue:

Se mide en ohminos mm2/metros
POTENCIA
La potencia eléctrica es la relación de paso de energía por unidad de tiempo; es decir, la cantidad de energía entregada o absorbida por un elemento en un tiempo determinado. En el sistema intenazional se mide en Watios.
ENERGÍA
Energía es la capacidad que tiene un mecanismo o dispositivo eléctrico cualquiera para realizar un trabajo
E = Pontencia x Tiempo ---> E = Watios x Hora
CIRCUITOS EN PARALELO
El circuito en paralelo es una conexión donde los bornes o terminales de entrada de todos los dispositivos (generadores, resistencias, condensadores, etc.) conectados coincidan entre sí, lo mismo que sus terminales de salida.
- 1/Req = 1/R1 + 1/R2 + 1/R3
- Intensidad = I1 = I2 = I3
- Voltaje total = V1 +V2 +V3 ----> V1 = I1 x R1 = Voltaje total
----> V2 = I2 x R2 = Voltaje total
---->V3 = I3 x R3 = Voltaje total

CIRCUITOS EN SERIE
Un circuito en serie es una configuración de conexión en la que los bornes o terminales de los dispositivos
(generadores, resistencias, condensadores, interruptores, entre otros.) se conectan secuencialmente. La terminal de salida de un dispositivo se conecta a la terminal de entrada del dispositivo siguiente.
- Resistencia = R1 +R2 + R3
- Intensidade total = I1 = I2 = I3
- Voltaje total = V1 + V2 + V3 ----> V1 = I1 x R1
----> V2 = I2 x R2
----> V3 = I3 x R3

CIRCUITOS MIXTOS
CONDENSADORES EN SERIE
1/ Ceq = 1/ C1 + 1/C2
CONDENSADORES EN PARALELO
Ceq = C1 + C2

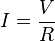
 Se mide en ohminos mm2/metros
Se mide en ohminos mm2/metros